The volume calculator provides the volume equations for numerous geometric shapes. Spherical Shapes The calculation allow the user to enter dimension in any of a large number of length units (SI, English, other).  

Description

This calculator contains the volume equations for a variety of geometric shapes. These equations allow the user to enter the dimensions of the geometric shape which are used to calculate the object's volume.  The shapes include:

• Cube
• Box or Cuboid
• Cone and Cone frustum
• Paraboloid
• Cylinder
• Prism
• Pyramid and Pyramid frustum
• Sphere, sphere cap and sphere slice
• Ellipsoid
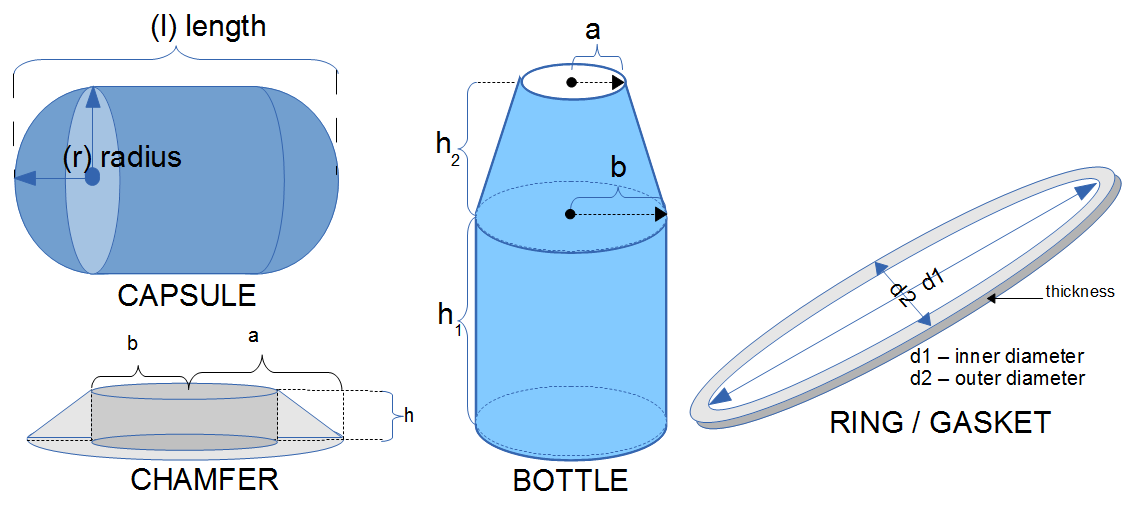
• Chamfer
• Ring (gasket / band)
• Capsule - combination of a sphere and a cylinder
• Bottle - combination of cone frustum and a cylinder

The third column of formulas computes the volume of polygon based columns ranging from a quadrilateral (4 sided) volume up to a dodecagon (12 sided) column.  The bases of these columns are regular polygons.  Regular polygons have equally length sides and equal interior angles.

The equations in this calculator are for the volume of different shapes.  Note that you can change the input units and that vCalc will manage the input and output volumes for you.  The equations let the user to enter the key dimensions needed to calculate the objects volume.

Volume

 common geometric combinations 
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance (solid, liquid, gas, or plasma) or shape occupies or contains.   Volume is often quantified numerically using the SI derived unit, the cubic meter. The volume of a container is generally understood to be the capacity of the container, i. e. the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces.

Three dimensional mathematical shapes are also assigned volumes. Volumes of some simple shapes, such as regular, straight-edged, and circular shapes can be easily calculated using arithmetic formulas.  Volumes of a complicated shape can be calculated by integral calculus if a formula exists for the shape's boundary.  Where a variance in shape and volume occurs, such as those that exist between different human beings, these can be calculated using three-dimensional techniques such as the Body Volume Index. various shapesOne-dimensional figures (such as lines) and two-dimensional shapes (such as squares) are assigned zero volume in the three-dimensional space.
Euclidean Shapes
The volume of a solid (whether regularly or irregularly shaped) can be determined by fluid displacement. Displacement of liquid can also be used to determine the volume of a gas. The combined volume of two substances is usually greater than the volume of one of the substances. However, sometimes one substance dissolves in the other and the combined volume is not additive.

In differential geometry, volume is expressed by means of the volume form, and is an important global Riemannian invariant. In thermodynamics, volume is a fundamental parameter, and is a conjugate variable to pressure. 

See Also

• Mass Weight Calculator enables the user to enter a mean density with the shape dimensions to calculate a mass (weight).
• Area - Calculator with area equations for different geometric shapes.
• Engine Calculator - Calculator with volume and ratio formulas for a combustion engine.
• Trucking Calculator -  Calculator with load weights and volumes for trucking containers.

References

• Wikipedia - http://en.wikipedia.org/wiki/Volume